SurveyMonkey
Cómo calcular la cantidad de respuestas que necesitas
La cantidad de encuestados que necesitas depende de los objetivos de la encuesta y de con cuánta seguridad quieres contar con los resultados. Cuánto más seguro quieras estar, menor margen de error deberías aceptar.
Para calcular la cantidad de encuestados que necesitas (conocido como el tamaño de la muestra), utiliza nuestra calculadora del tamaño de la muestra.
SUGERENCIA: Si necesitas una cantidad garantizada de encuestados, compra respuestas de la encuesta de SurveyMonkey Audience. Tú especificas la cantidad de respuestas que necesitas y nosotros utilizaremos los criterios que definas para buscar a los encuestados.
Definiciones
Para calcular el tamaño de la muestra, necesitarás contar con la siguiente información:
- Tamaño de la población
- Margen de error
- Nivel de confianza
- Valor del porcentaje
Cómo calcular el tamaño de la muestra
Calcula la cantidad de encuestados que necesitas en cuestión de segundos con nuestra calculadora del tamaño de la muestra. Si deseas realizar el cálculo del tamaño de la muestra en forma manual, utiliza la siguiente fórmula:
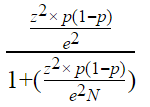
Estadística | Descripción |
| N | Tamaño de la población |
| e | Margen de error (como decimal) |
| z | Nivel de confianza (como puntuación de z) |
| p | Valor de porcentaje (como decimal) |
Tamaños de muestra sugeridos
A continuación, se incluye una tabla con los tamaños de población sugeridos* por margen de error a un nivel de confianza del 95 %. Utilizamos la fórmula anterior para calcular los tamaños de muestra sugeridos. En algunos casos, redondeamos los tamaños de las muestras al 5 o 10 más cercano. Para un cálculo más exacto, usa nuestra calculadora del tamaño de muestra.
| Tamaño de la población | Tamaño de la muestra por margen de error | Tamaño de la muestra por margen de error | Tamaño de la muestra por margen de error |
| ±3 % | ±5 % | ±10 % | |
| 500 | 345 | 220 | 80 |
| 1000 | 525 | 285 | 90 |
| 3000 | 810 | 350 | 100 |
| 5000 | 910 | 370 | 100 |
| 10 000 | 1000 | 385 | 100 |
| 100 000 | 1100 | 400 | 100 |
Ejemplo del tamaño de la muestra
Supongamos que envías una encuesta con una pregunta Sí o No, en la que se les plantea a los padres de los niños de la escuela si están a favor de tener una jornada escolar extendida.
La cantidad total de padres (el tamaño de la población) es de 10 000 y consideras un margen de error del ±10 %. Si utilizas la tabla de arriba, puedes ver que necesitas que al menos 100 personas respondan la encuesta.
El 70 % de los 100 padres encuestados manifestó estar a favor de la jornada escolar extendida. Con esto puedes asumir que, si 10 000 padres respondieran la encuesta, entre el 60 % y el 80 % de ellos estarían a favor de la jornada escolar extendida.
¿Cuántas personas deberían responder mi encuesta?
El índice de respuestas puede afectar la cantidad de personas a las que les envías la encuesta. Cuanto más alto el índice de respuestas, menos personas necesitas que responda la encuesta.
Por ejemplo, si necesitas 100 encuestados y esperas que el 25 % de las personas a las que invitaste a responder la encuesta realmente la responda, entonces necesitas invitar a 400 personas a que respondan la encuesta.
Para calcular la cantidad de personas que necesitas invitar a que respondan la encuesta en función del índice de respuestas esperado, aplica la siguiente ecuación:

Encuestados necesarios
Toma la cantidad de personas que necesitas para responder tu encuesta
÷ Índice de respuestas
Divide por el índice de respuestas esperado (usa 25 para el 25 %; si usas 0.25, omite el paso 3)
x 100
A continuación, multiplica por 100 (para tener en cuenta el uso de un porcentaje versus un decimal en el paso 2)